Las Matemáticas son tan antiguas como el propio conocimiento humano.
La aplicación de las matemáticas al estudio de la naturaleza se remonta a los griegos y, aplicadas a la botánica en concreto, han destacado numerosos científicos a lo largo de la historia como Leonardo de Pisa, Leonardo da Vinci, Galileo, Euler o Guido Grandi entre muchos otros.
El mundo vegetal tiene sus propias leyes físicas que condicionan el crecimiento y las formas de las plantas, que responden siempre a principios de optimización, economía de medios e interacción con el medio exterior. Las plantas hacen cálculos para saber cuánto alimento han de producir o cual es la altura máxima que han de alcanzar. Igualmente aplican cálculos para saber cuánta agua deben absorber.
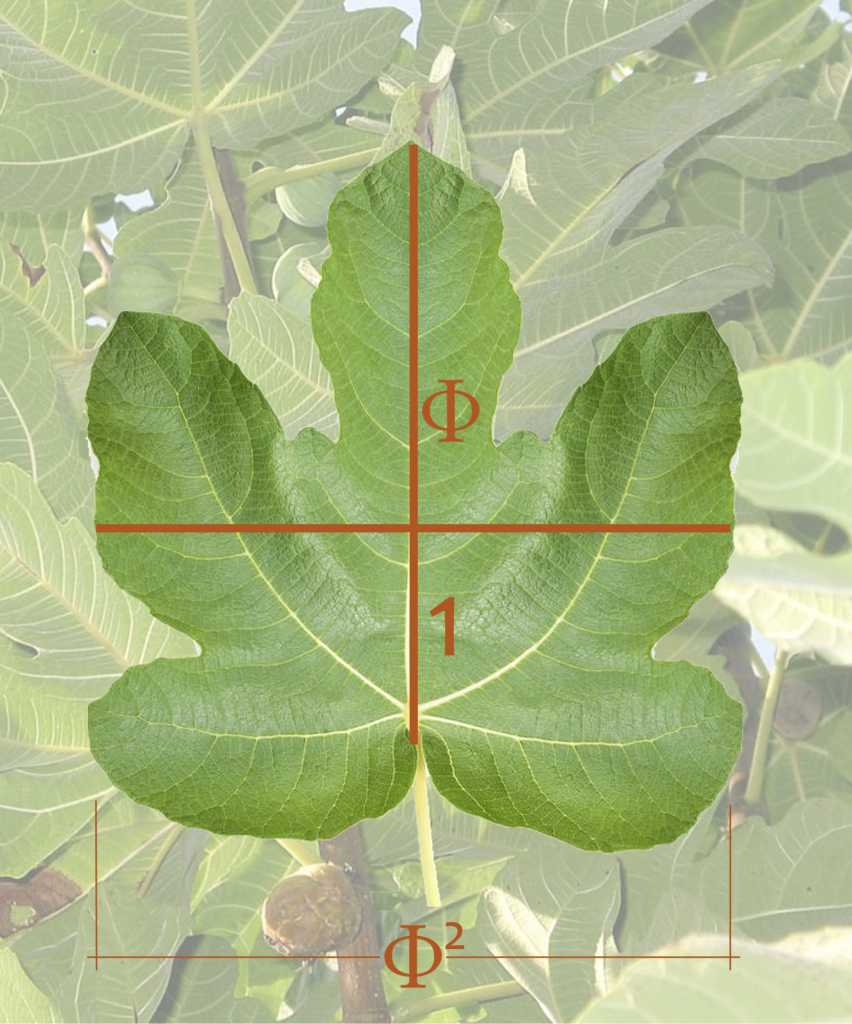
A medida que crecen, pueden generar formas geométricas asombrosamente regulares y complejas. Muchas de ellas guardan relación con la sucesión de Fibonacci y con el número áureo.
La situación de los pétalos en una flor responde a una ecuación matemática, la disposición de las ramas no es aleatoria, se disponen en base a un ángulo determinado para favorecer la llegada de los rayos de sol a todas sus hojas.
Existen algunos modelos matemáticos que describen buena parte de los distintos comportamientos de las plantas.
En el Jardín de lՓs MatemáticՓs se presentan muchas de estas relaciones botánico-matemáticas.
Cada relación matemática está representada por una escultura metálica y una o varias plantas, todo ello apoyado con carteles explicativos de estas relaciones. Además, como Jardín perteneciente a la colección de Jardines Botánicos de la Universidad de Almería, cada planta tiene su correspondiente cartel QR que enlazará con la página web del herbario de la UAL (HUAL), donde se explican todas las características botánicas de la planta, así como un QR matemático que enlaza con la página web elaborada por la Facultad de Ciencias Experimentales y el Departamento de Matemáticas que explica las características matemáticas.
El Jardín se sitúa alrededor del CITE III o Edificio de Matemáticas. Se encuentra dividido en diferentes parterres, cada uno de ellos correspondiente a un concepto matemátco: Fractal, Espiral, Hélice, Ángulos/Ángulo de Oro, Sucesión de Fibonacci, Número Aúreo, Geométricas, Concoide de Rosetón y Simetrías.
En uno de los parterres se ha plantado un árbol del género Melia, en concreto un Melia azedarach, que no va a ser podado en ningún momento y con el que podremos comprobar tanto la Regla de Da Vinci así como que sus ramas siguen la sucesión de Fibonacci.
Por último, tenemos un parterre “cajón de sastre”, donde se irán incluyendo diversos estudios relacionados con la Botánica y las Matemáticas, de manera que podamos estar siempre al día en los estudios científicos realizados en esta materia.
Es un Jardín no solo para disfrutar con la vista, el olfato y el tacto, es un jardín interactivo que ayuda al desarrollo de la inteligencia, a enfrentarse a retos, propiciar agilidad mental, reforzar capacidades lógicas, aprender a contemplar la naturaleza desde una nueva perspectiva…
Además, no está diseñado solo para la comunidad universitaria, su público potencial son todos los estudiantes, desde primaria a la universidad, profesionales de las matemáticas, amantes de los jardines temáticos y público en general.
Para la realización de este proyecto hemos contado con la colaboración de la Facultad de Ciencias Experimentales y del Departamento de Matemáticas, que han realizado no solo los textos que explican los conceptos matemáticos, también problemas, juegos y retos matemático-botánicos para que podamos disfrutar todo el potencial de este Jardín.

CONCEPTOS MATEMÁTICOS
Para conocer y ampliar los conceptos matemáticos pincha aquí y accederás a la página web elaborada por la Facultad de Ciencias Experimentales y el Departamento de Matemáticas.

PLANTAS MATEMÁTICAS
Puedes acceder a la galería de imágenes de este jardín pinchando aquí.
Junto al encabezado de cada planta encontrarás un símbolo que corresponde al concepto matemático que representa. Pinchando ese símbolo te llevará a la página web elaborada por la Facultad de Ciencias Experimentales y el Departamento de Matemáticas donde te explican ese concepto. Aquí tienes algunos ejemplos.

GEOMETRÍAS 
FRACTALES 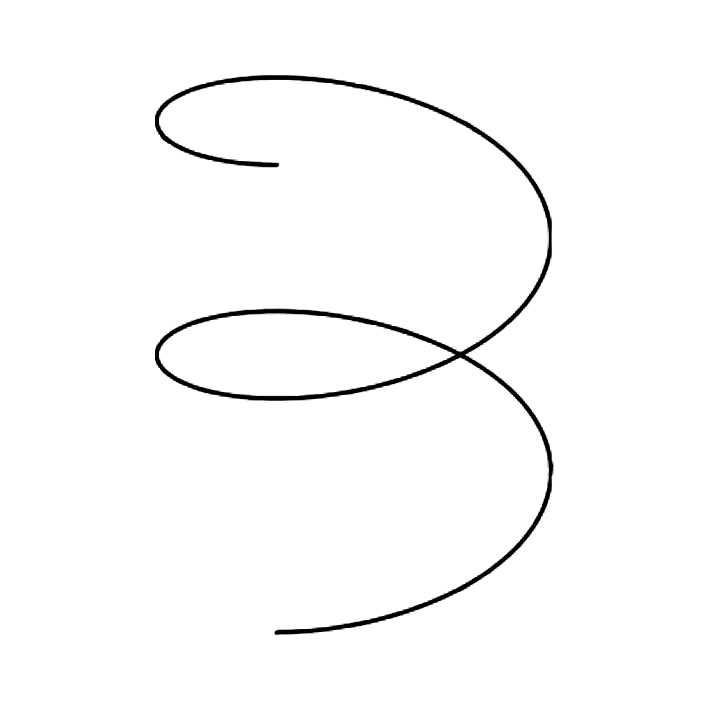
HÉLICES 
ESPIRALES 
ASIMETRÍA 
SIMETRÍA BILATERAL 
SIMETRÍA RADIAL 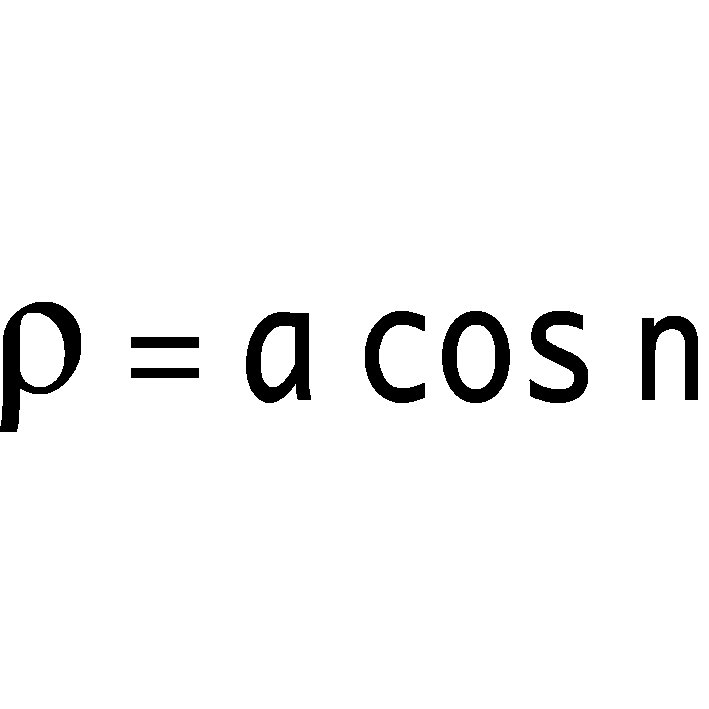
CONCOIDE DE ROSETÓN 
ÁNGULO AGUDO 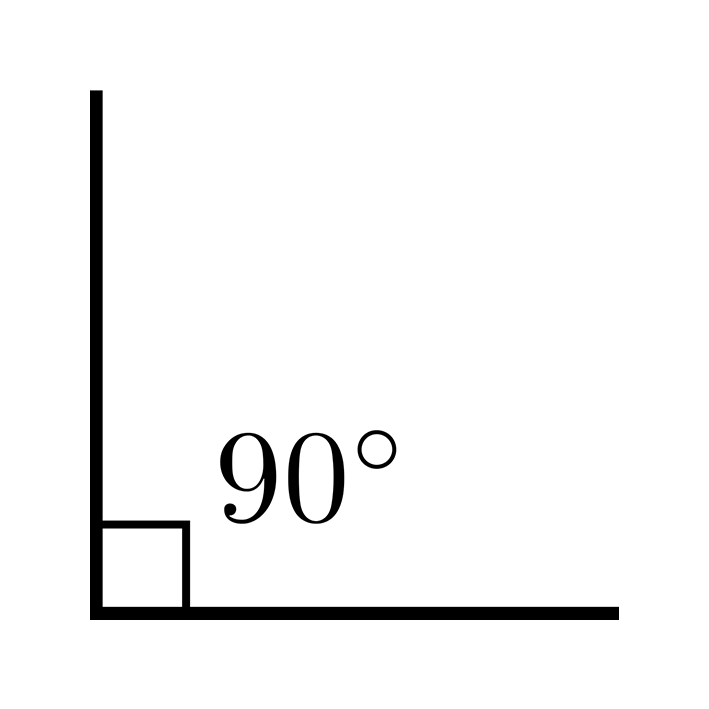
ÁNGULO RECTO 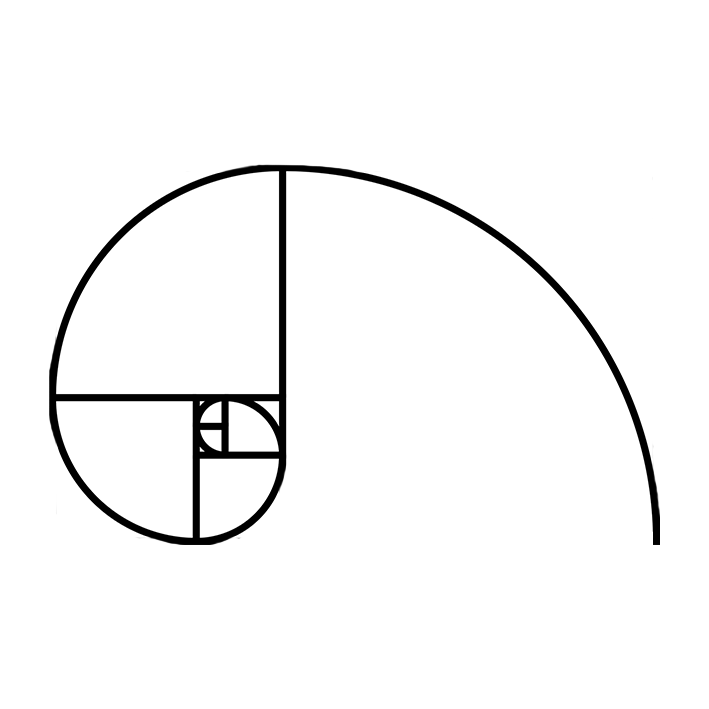
FIBONACCI 
CAJÓN DE SASTRE